We have here a linear problem. We can pose the problem using linear equations.
1. We know that Gabrielle can run 7 yards per second, and we can write this as follows:
G(t) = 7t (this is the function for the distance that Gabrielle runs.) Time is the independent variable (or this is a function of time.)
2. We know that Florence can run 8 yards per second, and we can write this as follows:
F(t) = 8t ((this is the function for the distance that Florence runs.)
3. But we know that Gabrielle starts with 17 yards since she runs more slowly.
Then, Gabrielle's equation is G(t) = 7t + 17.
To see where Florence catches up to Gabrielle, we need to equal both equations to find the time when they meet. Then, we have that:
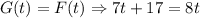
4. Now, we need to solve this equation:

Since the time is in seconds, we have that Florence and Gabrielle meet each other at 17 seconds after they started running.
To have how far Florence will have to run, we need to substitute this time in Florence's function:
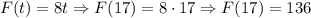
That is, Florence needs to run 136 yards to meet Gabrielle in these 17 seconds.
In summary:
How long will that take? 17 seconds.
How far will Florence have to run? 136 yards.