Question

The ratio of the volume of two spheres is 8: 27. What is the ratio of their radio?

Answer 1

Given:

The ratio of the volume of the two spheres is 8: 27.

Required:

To find the ratio of their radius.

Step-by-step explanation:

The volume of the sphere is given by the formula:

`V=(4)/(3)\pi r^3`

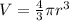
Where r = radius of the circle.

Let the radius of the spheres are

`r_1\text{ and r}_2`

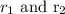
and volume are

`V_1\text{ and V}_2`
`\begin{gathered} (V_1)/(V_2)=((4)/(3)\pi r_1^3)/((4)/(3)\pi r_2^3) \\ (8)/(27)=(r_1^3)/(r_2^3) \end{gathered}`

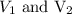
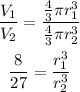
Take the cube root on both sides we get:

`\begin{gathered} (r_1)/(r_2)=\sqrt[3]{(8)/(27)} \\ (r_(1))/(r_(2))=\sqrt[3]{(2*2*2)/(3*3*3)} \\ (r_1)/(r_2)=(2)/(3) \end{gathered}`

The ratio of their radius is 2 : 3.

Final answer:

Thus option a is the correct answer.