Question

There is a need for lawn service in Short Pump. The need is great and Canada's Motley Crew Yard Geniusek is onthe job. The Geniuses will offer the following deal to a neighborhood offering a mow, trim and clean-up for thefollowing prices:20 yards at $5015 yards at $4010 yards at $305 yards at $20The neighborhood of Lucas Estates has decided that they should dictate prices and has offered the following tothe Crew:20 yards - $2015 yards - $3010 yards - $405 yards - $50What will be the equilibrium price?

Answer 1

Let,

x = length pf the lawn to work with

y = price offer

Step 1: Let's determine the equation of the Motley Crew Yard Geniusek's price.

Let's use,

x1,y1 = 5,20

x2,y2 = 10,30

Determining the slope, m

`\text{ m = }(y_2-y_1)/(x_2-x_1)`
`\text{ = }\frac{30\text{ - 20}}{10\text{ - 5}}\text{ = }(10)/(5)`
`\text{ m = 2}`

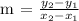
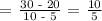
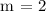
Determining the y-intercept, b

Use,

x,y = 5,20

m = 2

`\text{ y = mx + b}`
`\text{ 20 = 2(5) + b}`
`\text{ 20 = 10 + b}`
`\text{ 20 - 10 = b}`
`\text{ 10 = b}`

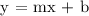
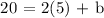
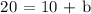
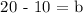
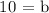
Completing the equation, m = 2 and y = 10:

`\text{ y = mx + b}`
`\text{ y = 2x + 1}0\text{ (Equation 1)}`

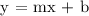
Step 2: Let's determine the equation of the Lucas Estates neighborhood's offered price.

Let's use,

x1,y1 = 5,50

x2,y2 = 10,40

Determining the slope, m

`\text{ m = }(y_2-y_1)/(x_2-x_1)`
`\text{ = }\frac{40\text{ - 50}}{10\text{ - 5}}\text{ = }(-10)/(5)`
`\text{ m = -2}`

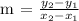
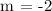
Determining the y-intercept, b

Use,

x,y = 5,50

m = -2

`\text{ y = mx + b}`
`\text{ 50 = (-2)(5) + b}`
`\text{ 50 = -10 + b}`
`\text{ 50 + 10 = b}`
`\text{ 60 = b}`

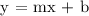
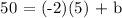
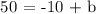
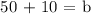
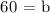
Completing the equation, m = -2 and b = 60:

`\text{ y = mx + b}`
`\text{ y = (-2)x + }60`
`\text{ y = -2x + 60 (Equation 2)}`

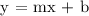
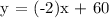
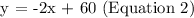
Step 3: Determining the equilibrium price, let's determine the length of the lawn that will match up to the price offer of Canada's Motley Crew Yard Geniusek and the neighborhood of Lucas Estates.

`\text{ y (Canada's Mostley Crew Yard Geniusek) = y (Lucas Estates neighborhood)}`
`\text{ 2x + 10 = -2x + 60}`
`\text{ 2x + 2x = 60 - 10}`
`\text{ 4x = 50}`
`\text{ }\frac{\text{4x}}{4}\text{ = }\frac{\text{50}}{4}`
`\text{ x = 12.50 yards}`

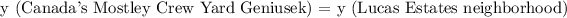
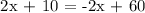
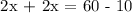
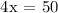
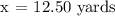
The price offer of the Geniusek and Lucas Estate neighborhood would be in equilibrium at 12.50 yards. Let's determine the price.

y = 2x + 10

y = 2(12.50) + 10

y = 25 + 10

y = $35

The equilibrium price will be $35 at 12.50 yards.