Question

What is the diameter of hemisphere with a volume of 841 cm^3 to the nearest tenth of a centimeter?

Answer 1

The rule of the volume of the hemisphere is

`V=(2)/(3)\pi r^3`

r is the radius of it

Since the diameter of the hemisphere is double the radius, then we can find the radius then multiply it by 2 to find it

Since the volume of the hemisphere is 841 cm^3, then

Substitute V by 841

`\begin{gathered} 841=(2)/(3)\pi(r^3) \\ 841=(2)/(3)\pi r^3 \end{gathered}`

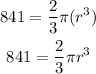
Divide both sides by 2/3pi

`\begin{gathered} (841)/((2)/(3)\pi)=((2)/(3)\pi r^3)/((2)/(3)\pi) \\ \\ (2523)/(2\pi)=r^3 \end{gathered}`

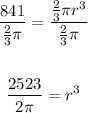
Take cube root to both sides

`\begin{gathered} \sqrt[3]{(2523)/(2\pi)}=\sqrt[3]{r^3} \\ 7.377555082=r \end{gathered}`

Multiply it by 2 to find the diameter, then round it to the nearest tenth

`\begin{gathered} d=7.377555082*2 \\ d=14.75511016 \\ d=14.8\text{ cm} \end{gathered}`

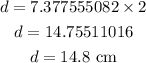
The diameter of the hemisphere is 14.8 cm