Question

This is the question I need help with. Find the vertices, foci, and asymptotes of a hyperbola with the equation:16x^2 - 4y^2 = 64. This is what I know so far. You divide both sides of the equation by 64 to have the equation equal to 0. That leaves you with the equationx^2/4 - y^2/16 = 1a^2 = 4 and the square root of that is 2. b^2 = 16 and the square root of that is 4. I used the pythagorean theorem to figure out that a^2 + b^2 = C^2 ------> 4 + 16 = 20.c^2 = 20 = 2 square root 5. But, now, I am stuck. How do we use that information to find the vertices, foci and asymptotes?

Answer 1

Let's write the standard form of a horizontal hyperbola equation:

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

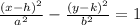
Where the center is located at (h, k), the vertices are located at (h±a, k), the foci are located at (h±c, k) and the asymptotes are:

`y=\pm(b)/(a)(x-h)+k`

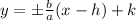
Comparing the standard form with the equation x^2/4 - y^2/16 = 1, we have:

h = 0, k = 0, a = 2 and b = 4.

The value of c was already calculated: c = 2√5.

Therefore the vertices are (-2, 0) and (2, 0), the foci are (-2√5, 0) and (2√5, 0) and the asymptotes are:

`y=\pm2x`