Question

Factor by grouping
`(8y ^3 - 20y ^2) - (6y + 15)`

Answer 1

We have two terms in this expression.

First let's remove the parenthesis:

`(8y^3-20y^2)-(6y+15)=8y^3-20y^2-6y-15`

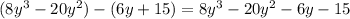
The first two terms can be factored with we put 4y^2 in evidence:

`8y^3-20y^2=4y^2(2y-5)`

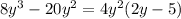
Then, in the other two terms we can put 3 in evidence:

`-6y-15=-3(2y+5)`

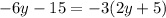
There aren't common factors between the expressions, so we can try to group other terms.

If we group 8y^3 and -6y, we have:

`8y^3-6y=2y(4y^2-3)`

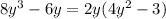
And grouping -20y^2 and -15, we have:

`-20y^2-15=-5(4y^2+3)`

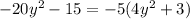
There aren't common factors between the expressions.

So two possibilities of factoring by grouping are:

`\begin{gathered} 4y^2(2y-5)-3(2y+5) \\ \text{and} \\ 2y(4y^2-3)-5(4y^2+3) \end{gathered}`