Question

How many solutions are there for the system shown below? х+у= 25 ху = -5 ОА. 1 ов. 4 ОО ос. з OD D. 2 о

Answer 1

Choice D. 2 solutions

Step-by-step explanation:

Adding the two equations gives

`\begin{gathered} x^2+y^2=25 \\ x-y^2=-5 \\ --------- \\ x^2+x=20 \end{gathered}`

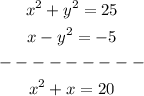
Therefore, we have the quadratic equations

`x^2+x-20=0`

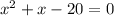
which has the solutions ( using quadratic formula)

`x=\frac{-1\pm\sqrt[]{1^2-4(1)(-20)}}{2}`
`x=\frac{-1\pm\sqrt[]{81}}{2}`

meaning we have two values of x that satisfy the system of equations.

Therefore, choice D is the correct answer.