Question

16) How many photons are contained in a burst of yellow light (589 nm) from a sodium lamp that contains 609 kJ of energy?

A) 3.37 × 1019 photons
B) 3.06 × 1030 photons
C) 1.81 × 1024 photons
D) 4.03 × 1028 photons
E) 2.48 × 1025 photons

Answer 1

The correct answer to this question is this one:

find the energy of one photon:

E=h*c/λ

divide the energy given by the energy of one photon of that wavelength

What I've done so far is convert wave length to m and energy to j.

E photon = h * x / wave length
E = (6.626 x 10^-43)(3.00 x 10^8) / 587 ^ -9 = 3.38 x 10 ^18 J
3.38 x 10 ^18 J x 1000 kj / 1 j = 3.37 x 10 ^ 16 Kj
609 kJ/ 3.37 x 10 ^ 16 Kj = 1.81 x 10 ^ 16

E = (6.626 x 10^-34)(3.00 x 10^8) / 587 ^ -9 = 3.38 x 10 ^19 J
3.38 x 10 ^19 J x 1000 kj / 1 j = 3.37 x 10 ^ -16 Kj
609 kJ/ 3.37 x 10 ^ 16 Kj = 1.81 x 10 ^ 18 but the answer is 1.81 × 10^24 photons

3.38 x 10 ^-19 J
should be negative

then 3.38 x 10 ^18 J x 1kJ/1000 J

you're converting from J to kJ.. just like meters to kilometres, you wouldn't multiply you would divide

Answer 2

Answer: C)
`1.81* 10^(24)` photons

Step-by-step explanation:

`E=(nhc)/(\lambda)`

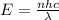
E= energy = 609 kJ = 609000 J (1kJ=1000J)

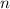`n` = number of photons = ?

h = Planck's constant =
`6.626* 10^(-34)Js`

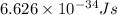
c = speed of light =
`3* 10^8m/s`

`\lambda` = wavelength of photon = 589 nm =
`589* 10^(-9)m`

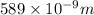
Putting values in above equation, we get:

`609000J=(n* (6.626* 10^(-34)Js)* (3* 10^8m/s))/(589* 10^(-9)m)`

`n=1.81* 10^(24)`

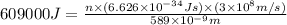
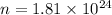
Thus there are
`1.81* 10^(24)` photons in a burst of yellow light (589 nm) from a sodium lamp that contains 609 kJ of energy.