Given:
The quadratic equation is
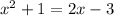
To find:
The expression that correctly sets up the quadratic formula with the given equation.
Solution:
We have,
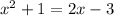
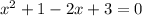
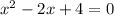
On comparing with
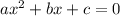 , we get
, we get
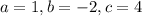
The quadratic formula is
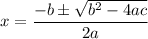
Putting
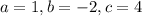 , we get
, we get
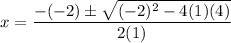
Therefore, the required expression is
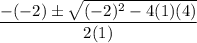 .
.