Question

A manufacturer knows that their items have a lengths that are skewed right, with a mean of 9.4 inches, andstandard deviation of 3 inches.If 36 items are chosen at random, what is the probability that their mean length is greater than 10.6 inches?(Round answer to four decimal places)

Answer 1

We can suppose that when taking a sample of a variable that has a skewed distribution, this skewness is less important and we can approximate it to a normal.

If we take a sample of 36 items (n=36) from a distribution that has a mean of 9.4 in. and standard deviation of 3 in., and we want to calculate the probability that their mean length is greater than 10.6 in. (X=10.6), we start by calculating the z-score:

`z=\frac{X-\mu}{\frac{\sigma}{\sqrt[]{n}}}=\frac{10.6-9.4}{\frac{3}{\sqrt[]{36}}}=(1.2)/((3)/(6))=(1.2)/(0.5)=2.4`

If we approximate the sample mean distribution as a normal distribution, we can calculate the probability as:

`P(X>10.6)=P(z>2.4)\approx0.0082`

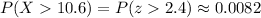
Answer: The probability that the sample mean is greater than 10.6 is approximately P(X>10.6) = 0.0082.