Question

Two friends are carrying a 200 kg crate up a flight of stairs. The crate is 1.25 m long and 0.500 m high, and its center of gravity is at its center. The stairs make a 45.0∘ angle with respect to the floor. The crate also is carried at a 45.0∘ angle, so that its bottom side is parallel to the slope of the stairs (Figure 1).What is the magnitude of the force applied by the person below?

Answer 1

Given:

Mass of crate = 200 kg

Length of crate = 1.25 m

Height of crate = 0.500 m

Angle the stairs make with respect to the floor = 45.0 degrees

Angle the crate is carried = 45 degrees

Let's find the magnitude of the force applied by the person below.

Let's first make a free body diagram representing this situation:

Where:

FL represents the force applied by the person below

Fu represents the force applied by the person above.

`\begin{gathered} \Sigma Fy=0 \\ \\ mg=F_U+F_L \end{gathered}`

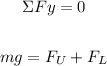
We have:

`mg=200*9.8=1960\text{ N}`

Now to find the magnitude of force applied by the person below, we have:

`\Sigma m=mg((1.25)/(2)-0.25)cos45-F_U*1.25cos45=0`

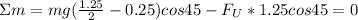
Since the sum of the moments around the bottom must be zero.

Thus, we have:

`\begin{gathered} F_U=(1960((1.25)/(2)-0.25)cos45)/(1.25cos45) \\ \\ F_U=(1960(0.375)cos45)/(1.25cos45) \\ \\ F_U=588\text{ N} \end{gathered}`

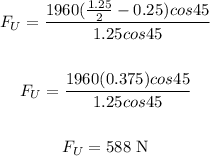
The force applied by the person above is 588 N.

Thus, the force applied by the person below will be:

`\begin{gathered} F_L=-F_U+mg \\ \\ F_L=-588+200*9.8 \\ \\ F_L=-588+1960 \\ \\ F_U=1372\text{ N} \end{gathered}`

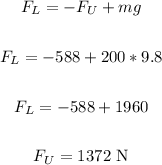
Therefore, the magnitude of the force applied by the person below is 1372 N.

ANSWER:

1372 N.