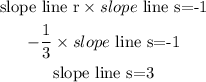A line parallel to each given line will have equal slopes. Lines perpendicular to each other have the product of their slopes equal to -1. We can summarize like this:
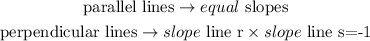
Let's do the math and get each slope.
The slope of a line can be calculated using the formula:
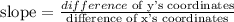
1.
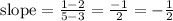
So we have:
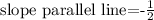
And
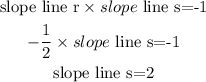
2.
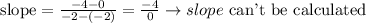
On this case, we have a perpendicular line to the x-axis.
A parallel line to this can be any vertical line which equation is:
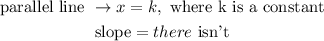
A perpendicular line to this can be any horizontal line which equation is:
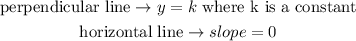
3.
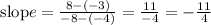
Then
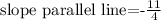
And
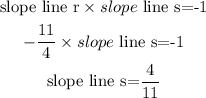
4.
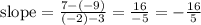
Then
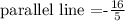
And
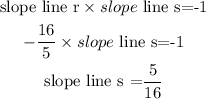
5.
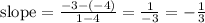
Then

And