Question

(i) Modulus of a complex number Z is 2 and arg(Z) =pi/3 Write the complex number 1 3 in the form a + ib.

Answer 1

The complex number a+ib is;

`1+i\sqrt[]{3}`

Step-by-step explanation:

Given the complex number;

`a+ib`

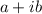
The modulus of the complex number is given as;

`\begin{gathered} \sqrt[]{a^2+b^2}=2 \\ a^2+b^2=2^2 \\ a^2+b^2=4 \\ a^2=4-b^2\text{ -------- 1} \end{gathered}`

Also the argument of the complex number;

`\begin{gathered} arg(z)=\tan ^(-1)((b)/(a))=(\pi)/(3) \\ (b)/(a)=\tan ((\pi)/(3)) \\ (b)/(a)=\sqrt[]{3} \\ b=a\sqrt[]{3}--------2 \end{gathered}`

substituting equation 2 into equation 1;

`\begin{gathered} a^2=4-b^2\text{ } \\ a^2=4-(a\sqrt[]{3})^2\text{ } \\ a^2=4-a^2(3) \\ a^2+3a^2=4 \\ 4a^2=4 \\ a^2=(4)/(4) \\ a^2=1 \\ a=1 \end{gathered}`

Substituting a=1 into equation 2;

`\begin{gathered} b=a\sqrt[]{3} \\ b=1*\sqrt[]{3} \\ b=\sqrt[]{3} \end{gathered}`

Therefore, the complex number a+ib is;

`1+i\sqrt[]{3}`