Question

A rectangle has a length of 30 feet less than 6 times its width. If the area of the rectangle is 4836 square feet, find the length of the rectangle.Answer How to enter your answer (opens in new window) 5 PointsКеурасKeyboard Shortcufeet

Answer 1

Explanation

Variables

• x: width of the rectangle, in ft

,

• y: length of the rectangle, in ft

Given that the length, y, is 30 feet less than 6 times the width, x, then:

`y=6x-30\text{ \lparen eq. 1\rparen}`

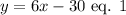
The area of a rectangle is calculated as follows:

`Area=length{}t* width`

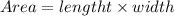
In this case, the area is 4836 square ft. Substituting this value and using the before defined variables, we get:

`4836=yx\text{ \lparen eq. 2\rparen}`

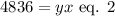
Substituting equation 1 into equation 2:

`\begin{gathered} 4836=(6x-30)x \\ 4,836=6x^2-30x \\ 0=6x^2-30x-4836 \end{gathered}`

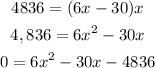
We can solve this equation with the help of the quadratic formula, as follows:

`\begin{gathered} x_(1,2)=(-b\pm√(b^2-4ac))/(2a) \\ x_(1,2)=(3^0\pm√((-30)^2-4\cdot6\cdot(-4836)))/(2\cdot6)\frac{}{} \\ x_(1,2)=(30\pm√(116964))/(12) \\ x_(1,2)=(30\pm342)/(12) \\ x_1=(30+342)/(12)=31 \\ x_2=(30-342)/(12)=-26 \end{gathered}`

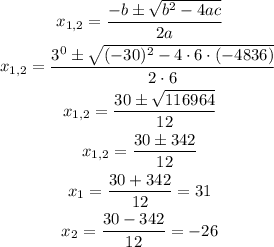
Given that the width cannot be negative, then the second solution is discarded.

Substituting x = 31 ft into equation 1: