Local minimum and maximum
Local extrema and relative extrema are synonyms that refer to the points with the y-values that are the highest or the lowest y-values on a local neighborhood of the domain of a function. Let us represent graphically this situation
In the figure above we have both classes of points,
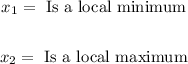
The reason why x_1 is a local minimum, is because locally, the function f(x) takes its lowest value at x_1
The reason why x_w=2 is a local maximum, is because the function f(x) take its highest locally y-value at x_2
The term local is better explained with a draw
In the graph above, we have four local extrema points, with the following specifications

From the graph we cannot determine who has the highest y-value between x_1 and x_3, but this information is irrelevant to define them as local maximum, because we are certain that for points near of x_1, the y-value of x_1 is the highest, this is why we say that x_1 is a local maximum, seemingly analysis can be applied to all the other local extrema x_2,x_3 and x_4.
They all are the highest or the lowest but when compared with their nearest neighbors , that is, they are maximum or minimum but locally ,