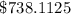Question

Show all the stepsRobin bought a computer for $1,250. It will depreciate, or decrease in value, by 10% each year that she owns it.* Is the sequence formed by the value at the beginning of each year arithmetic, geometric, or neither? Explain.* Write an explicit formula to represent the sequence.* Find the value of the computer at the beginning of the 6th year.

Answer 1

Given that:

- The value of the computer when Robin bought it was $1,250.

- Its value will decrease by 10% each year that she owns it.

• You can identify that the first term of the sequence is:

`a_1=1250`

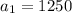
Knowing that it will depreciate by 10% each year, you can set up that the second term is (remember that a percent must be divided by 100 in order to write it in decimal form):

`a_2=1250-(1250)((10)/(100))`
`\begin{gathered} a_2=1250-(1250)(0.1) \\ \\ a_2=1250-125 \\ \\ a_2=1125 \end{gathered}`

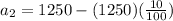
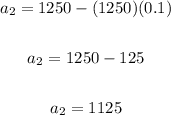
Notice that the third term is:

`\begin{gathered} a_3=a_2-(a_2)(0.1) \\ \\ a_3=1125-(1125)(0.1) \end{gathered}`
`a_3=1012.5`

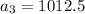
And the fourth term:

`\begin{gathered} a_4=a_3-(a_3)(0.1) \\ \\ a_4=1012.5-(1012.5)(0.1) \\ \\ a_4=911.25 \end{gathered}`

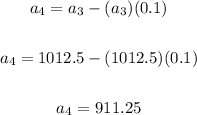
By definition, a term of a Geometric Sequence is obtained by multiplying the previous term by a constant called Common Ratio.

Therefore, you can check it this sequence is geometric as follows by identifying if there is a Common Ratio:

`\begin{gathered} (a_4)/(a_3)=(911.25)/(1012.5)=0.9 \\ \\ (a_3)/(a_2)=(1012.5)/(1125)=0.9 \\ \\ (a_2)/(a_1)=(1125)/(1250)=0.9 \end{gathered}`

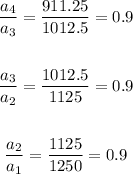
Notice that there is a Common Ratio:

`r=0.9`

Therefore, it is a Geometric Sequence.

• By definition, the Explicit Formula of a Geometric Sequence has this form:

`a_n=a_1\cdot r^(n-1)`

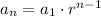
Where:

- The nth term is:

`a_n`

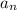
- The first term is:

`a_1`

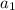
- The Common Ratio is:

`r`

- The term position is:

`n`

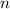
In this case, you already know the value of the first term and the Common Ratio. Therefore, you can substitute them into the formula in order to represent the sequence:

`a_n=(1250)(0.9)^(n-1)`

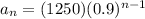
• In order to find the value of the computer at the beginning of the 6th year, you need to find the sixth term of the sequence:

`a_6`

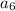
Therefore, you have to substitute this value of "n" into the Explicit Formula that represents the sequence and evaluate:

`n=6`

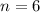
Then, you get:

`\begin{gathered} a_6=(1250)(0.9)^((6)-1) \\ a_6=(1250)(0.9)^5 \\ a_6=738.1125 \end{gathered}`

Hence, the answers are:

• It is a Geometric Sequence because it has a Common Ratio.

,

• Explicit Formula:

`a_n=(1250)(0.9)^(n-1)`

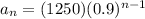
• Value of the computer at the beginning of the 6th year:

`\text{ \$}738.1125`