Question

The 4 kg bob swings on a massless cable 2 meters in length. Determine the velocity of the swinging pendulum at the instant = 33 degrees and the cable tension is 60 N. Report the result in m/s.

Answer 1

The given problem can be exemplified in the following diagram:

To determine the velocity when the mass is located at point 2 we will consider that the change in gravitational potential energy from 1 to 2 is equal to the kinetic energy at 2, therefore, we have:

`\Delta U=K`

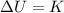
Where:

`\begin{gathered} \Delta U=\text{ change in gravitational potential energy} \\ K=\text{ kinetic energy} \end{gathered}`

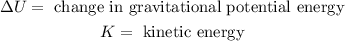
Now, we use the following formula for the gravitational potential energy:

`\Delta U=mgh`

Where:

`\begin{gathered} m=\text{ mass} \\ g=\text{ acceleration of gravity} \\ h=\text{ change in height} \end{gathered}`

The kinetic energy is given by:

`K=(1)/(2)mv^2`

Now, we substitute the formulas:

`mgh=(1)/(2)mv^2`

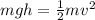
We can cancel out the mass "m":

`gh=(1)/(2)v^2`

Now, we solve for the velocity by multiplying both sides by 2:

`2gh=v^2`

Now, we take the square root to both sides:

`\sqrt[]{2gh}=v`

Now, we determine the height "h" using the following triangle:

We notice that the adjacent side of the triangle plus the height "h" is equal to the length of the pendulum, therefore, we have the next relationship:

`x+h=2`

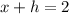
We solve for "h" by subtracting "x" from both sides:

`h=2-x`

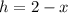
Now, we determine the value of "x" by using the function cosine:

`\cos 33=(x)/(2)`

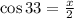
Now, we multiply both sides by 2:

`2\cos 33=x`

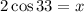
Now, we substitute the value of "x":

`h=2-2\cos 33`

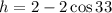
Solving the operations:

`h=0.32`

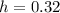
Therefore, the change in height is 0.32 meters. Substituting in the formula for the velocity we get:

`\sqrt[]{2(9.8(m)/(s^2))(0.32m)}=v`

Solving the operations:

`2.5(m)/(s)=v`

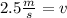
Therefore, the velocity of the mass is 2.5 m/s.