Question

the terminal ray of ∠A passes through the point (10,−4).∠A is drawn in standard position.What is the value of secA?Enter your answer as an exact answer, in simplified form, in the box.

Answer 1

Answer: the answer is √29/5

or (√25)/5 if you're confused so √ only 25 then divide that like the image shows below.

Explanation:

Answer 2

√29/5

Explanation:

The terminal ray of ∠A passes through the point (10,−4).

From the diagram above, angle A is in quadrant IV.

First, find the value of r using the Pythagoras theorem:

`\begin{gathered} r^2=10^2+(-4)^2 \\ r^2=100+16 \\ r^2=116 \\ r=√(116) \\ r=2√(29) \end{gathered}`

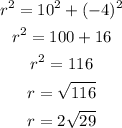
Secant is the inverse of cosine.

Therefore:

`\begin{gathered} \sec A=(Hypotenuse)/(Adjacent) \\ =(r)/(x) \\ =(2√(29))/(10) \\ \sec A=(√(29))/(5) \end{gathered}`

The value of sec A is √29/5.

Method 2

The terminal ray of ∠A passes through the point (10,−4).

`\begin{gathered} (x,y)=(10,-4) \\ \text{ Opposite Side, }y=-4 \\ \text{ Adjacent Side, }x=10 \end{gathered}`

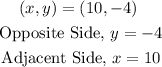
Find the value of the hypotenuse, r using the Pythagoras theorem:

`\begin{gathered} r^2=10^2+(-4)^2 \\ r^2=100+16 \\ r^2=116 \\ r=√(116) \\ r=2√(29) \end{gathered}`

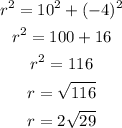
Secant is the inverse of cosine.

Therefore:

`\begin{gathered} \sec A=(Hypotenuse)/(Adjacent) \\ =(r)/(x) \\ =(2√(29))/(10) \\ \sec A=(√(29))/(5) \end{gathered}`

The value of sec A is √29/5.