Question

Logarithm 4) 20 grams of an unknown compound decays continuously according to the model A = A0e^-kt where A is the amount of compound remaining after + years. If the compound decays at a yearlyrate of 2%, how long before the amount of compound reaches one-fourth of its originalamount?

Answer 1

We know that the function describing the amount remaining is given by:

`A=A_0e^(-kt)`

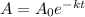
In this case the initial amount is 20 and the decay rate is 0.02 in decimal form, hence the function we need is:

`A=20e^(-0.02t)`

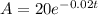
We want to know how long until the compound reaches one fourth of the original amount, this means that we need to find the time it takes to have 5 gr of the compond. Plugging this value in the function and solving for t we have:

`\begin{gathered} 5=20e^(-0.02t) \\ e^(-0.02t)=(5)/(20) \\ e^(-0.02t)=(1)/(4) \\ \ln e^(-0.02t)=\ln ((1)/(4)) \\ -0.02t=\ln ((1)/(4)) \\ t=-(1)/(0.02)\ln ((1)/(4)) \\ t=69.31 \end{gathered}`

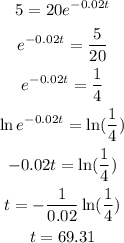
Therefore it takes approximately 69 years to have one forth of the orginal amount.