Question

Newton's law of cooling is T = Ae-h1+ C, where is the temperature of the object at time t, and C is the constant temperature of the surrounding medium. Supposethat the room temperature is 73, and the temperature of a cup of coffee is 174 when it is placed on the table. How long will it take for the coffee to cool to 131' fork = 0.0688919? Round your answer to two decimal places.

Answer 1

We have the Newton's law of cooling:

`T=Ae^(-kt)+C`

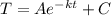
where:

A: initial difference of temperature between the object and the room temperature.

C: room temperature.

k: constant of cooling.

T: temperature of the object at time t.

We know that the initial temperature of the coffee is A+C = 174° and the room temperature is C = 73°.

Given a constant k = 0.0688919, we have to calculate the time t for which the coffe temperature T is 131°.

We can solve it as:

`\begin{gathered} T=131 \\ Ae^(-kt)+C=131 \\ (174-73)e^(-0.0688919t)+79=131 \\ 101e^(-0.0688919t)=131-79 \\ (101)/(101)e^(-0.0688919t)=(52)/(101) \\ \ln(e^(-0.0688919t))=\ln((52)/(101)) \\ -0.0688919t\approx-0.6638768 \\ t\approx(-0.6638768)/(-0.0688919) \\ t\approx9.64 \end{gathered}`

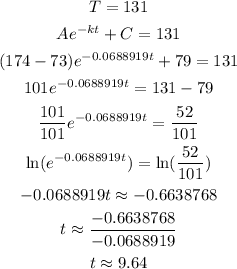
Answer: 9.64 minutes.