Question

What degree of rotation about the origin will cause the triangle below to maponto itself?000242+X2 468A-2-2 +-4B-6-8

Answer 1

We have a triangle in the third quadrant that we are going to rotate about the origin. If we perform a 90° rotation the triangle will map to the fourth quadrant so it won't map to itself. With 180° and 270° rotations it will map to the first and second quadrant respectively so, again, it won't map to itself. This means that we have only one option left, a 360° rotation. Let's check if it's correct. Performing a theta degrees rotation about the origin for a given point (a,b) maps it to point (c,d):

`\begin{gathered} c=a\cdot\cos \theta-b\cdot\sin \theta \\ d=a\cdot\sin \theta+b\cdot\cos \theta \end{gathered}`

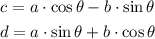
If the rotation angle is 360° then we have:

`\begin{gathered} c=a\cdot\cos 360^(\circ)-b\cdot\sin 360^(\circ) \\ d=a\cdot\sin 360^(\circ)+b\cdot\cos 360^(\circ) \\ c=a\cdot1+b\cdot0 \\ d=a\cdot0+b\cdot1 \\ c=a \\ d=b \end{gathered}`

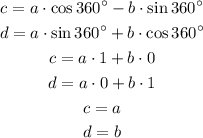
This means that (a,b)=(c,d) so after a 360° rotation any point maps to itself. This means that the triangle maps to itself after a 360° rotation and that's the correct answer.