Question

The larger of two numbers is 10 more than 3 times the smaller number. The difference between the two numbers is 28. What is the sum of the two numbers?

Answer 1

Let:

• x ,be the large number

,

• y, be the small number

"The larger of two numbers is 10 more than 3 times the smaller number"

means:

`x=3y+10`

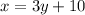
And

"The difference between the two numbers is 28"

means:

`x-y=28`

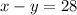
Notice that we get the following system of equations:

`\begin{cases}x=3y+10 \\ x-y=28\end{cases}`

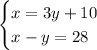
Now, let's subtitute equation 1 into equation 2 and solve for y :

`\begin{gathered} x-y=28 \\ \rightarrow3y+10-y=28 \\ \rightarrow2y=18\rightarrow y=(18)/(2) \\ \rightarrow y=9 \end{gathered}`

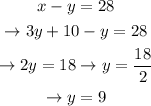
Now, substituting in equation 1 and solving for x :

`\begin{gathered} x=3y+10 \\ \rightarrow x=3(9)+10 \\ \rightarrow x=37 \end{gathered}`

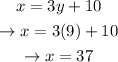
This way, we can conclide that both numbers are 37 and 9, and that their sum

`x+y\rightarrow37+9\rightarrow46`

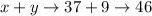
is 46