Question

A circle has a diameter of

18
m. Find the area of the sector
whose central angle is 135°

Answer 1

`\boxed {\boxed {\sf ( 243)/(8) \pi , 95.3775, or \ 95.42587686 \ m^2 }}`

Explanation:

When given the central angle in degrees, the formula for sector area is:

`A=( \theta)/(360) * \pi r^2`

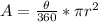
where θ is the central angle and r is the radius.

We are given the diameter, so we must calculate the radius. The radius is half the diameter.

• r= d/2

The diameter is 18 meters.

• r= 18 m/2
• r= 9 m

Now we know all the variables:

• θ=135

• r= 9 m

Substitute the values into the formula.

`A=( 135)/(360) * \pi (9)^2`

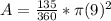
Solve the exponent first.

• (9)²= 9 m *9 m= 81 m²

`A=( 135)/(360) * (81 \ m^2) \pi`

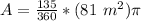
Solve the fraction.

`A=( 3)/(8) * (81 \ m^2) \pi`

Multiply the two rational numbers.

`A=(243)/(8) \pi \ m^2`

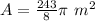
The answer can be left like this, in terms of pi, or can be multiplied.

1. Using 3.14 as pi

`A=(243)/(8) *3.14 \ m^2`

`A= 95.3775 \ m^2`

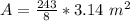
1. Using the pi button as pi

`A= 95.42587685 \ m^2`

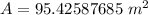
The area is 243/8 π, 95.3775, or 95.42587685 square meters.