Answer:
The solution of
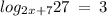 is -2.
is -2.
Explanation:
Given :
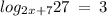
We have to solve for x.
Consider the given expression
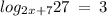
Apply rule,
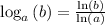
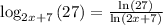
On simplifying, we get,
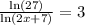
Multiply both side by
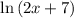
We have,
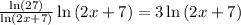
Multiply fractions as
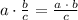
we get,
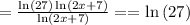
Thus, becomes
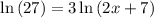
Divide both sides by 3, we have,
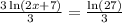
Apply rule
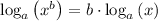
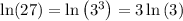
Thus,
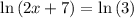
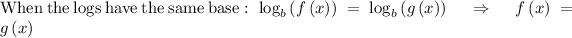
2x+ 7 = 3
Subtract 7 both sides, we get,
2x = 3 - 7
Simplify , we have,
2x = -4
Divide both side by 2, we have
x = -2
Thus, the solution of
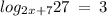 is -2.
is -2.