Question

Can you solve by steps and show me the focus equation please?

Answer 1

the length of the rectangular base is 2.5 times of width

let the width is b = x

then length is l = 2.5x

the volume of the box is 650 cm^2

let the height is h

so volume is

l x b x h = 650

(2.5x) (x) h = 650

h = 650/2.5x^2650

now the area of the base is

`\begin{gathered} A=x*2.5x \\ A=2.5x^2 \end{gathered}`

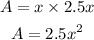
the cost of the base is 6 cents/ cm^2

now the total cost is,

6 (2.5x^2) = 15x^2

area of the sides is

A= 4 (l x h)

`\begin{gathered} A=4*2.5x* h \\ A=10x* h \end{gathered}`

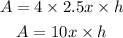
cost of the side is 6 cents/ cm^2

so total cost os sides are (10x)h

so total cost of the box is

15x^2 + 10xh

now, put the value of h

`\begin{gathered} =15x^2+10x*(650)/(2.5x^2) \\ =15x^2+(4*650)/(x) \end{gathered}`

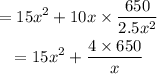
for minimizing the cost

differentiate the above expression

30x - 2600/x^2 =0

from here x = 4.42

now the dimension are

b= 4.42

l = 2.5 x 4.42 = 11.05

h = 13.30