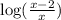Question

Use properties of logarithms to write each expression as a single term. Log (x-2) - log x

Answer 1

The original unsimplified expression is given to be:

`\log (x-2)-\log x`

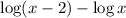
We can apply the Quotient Rule, one of the 7 Laws of Logarithms.

The Quotient Rule states that the logarithm of the ratio of two quantities is the logarithm of the numerator minus the logarithm of the denominator. Mathematically, this is written out as:

`\log _aM-\log _aN=\log _a((M)/(N))`

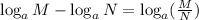
In our question, the bases of both logarithmic quantities are the same (base 10, since it's unspecified). Therefore, we can have the simplified expression to be:

`\log (x-2)-\log x=\log ((x-2)/(x))`

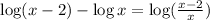
The answer is:

`\log ((x-2)/(x))`