Question

Use algebra to solve the following equations. Round decimals two places.a) 10 • log2(x) = 20b) 25e^4x= 5

Answer 1

We want to solve the following expressions

`\begin{gathered} 10\log _2x=20 \\ 25e^(4x)=5 \end{gathered}`

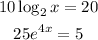
To solve the first expression

`10\log _2x=20`

We can start by dividing both sides by 10.

`\begin{gathered} (10\log_2x)/(10)=(20)/(10) \\ \log _2x=2 \end{gathered}`

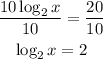
Using the following property

`a^b=c^(b\log _ca)`

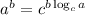
If we use both sides of our expression as exponents for a base 2 exponential, we can rewrite our expression as

`\begin{gathered} \log _2x=2 \\ 2^(\log _2x)=2^2 \\ x=2^2 \\ x=4 \end{gathered}`

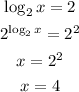
And this is the answer for the first expression. x = 4.

Solving the second expression

`25e^(4x)=5`

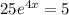
We can start by dividing both sides by 25.

`\begin{gathered} (25e^(4x))/(25)=(5)/(25) \\ e^(4x)=(1)/(5) \end{gathered}`

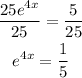
We can apply the natural log on both sides of our expression

`\begin{gathered} e^(4x)=(1)/(5) \\ \ln e^(4x)=\ln (1)/(5) \end{gathered}`

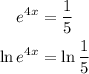
Using the following property

`\log _aa^b=b`

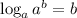
We can rewrite our expression as

`\begin{gathered} \ln e^(4x)=\ln (1)/(5) \\ 4x=\ln (1)/(5) \end{gathered}`

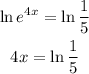
Dividing both sides by 4, we have

`\begin{gathered} 4x=\ln (1)/(5) \\ (4x)/(4)=(1)/(4)\cdot\ln (1)/(5) \\ x=(1)/(4)\ln (1)/(5) \end{gathered}`

We can simplify this expression by using the following properties

`\begin{gathered} \log a^b=b\log a \\ (1)/(a^b)=a^(-b) \end{gathered}`

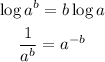
Simplifying our expression, we have

`\begin{gathered} x=(1)/(4)\ln (1)/(5) \\ x=(1)/(4)\ln 5^(-1) \\ x=-(\ln 5)/(4) \end{gathered}`

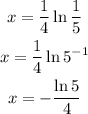
Using a calculator, we have

`x=-(\ln5)/(4)=-0.4023594781\cdots\approx-0.40`

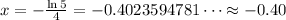
x = -0.40.