Answer:
x = 3, y = 6, and z = *1
Step-by-step explanation:
The substitution methods ask that we solve for one or two variables in one equation and substitute its value in the second equation.
For example, take the set of equations we are given to solve for x, y, and z:
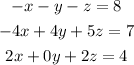
Now we take a look at the third equation.
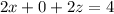
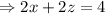
dividing both sides by 2 gives
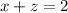
further multiplying both sides by -1 gives
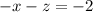
Now we substitute this value into -1x -1y -1z = -8.
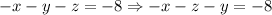
substitution gives
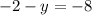
Now we can solve for y:
adding 2 to both sides gives
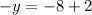

which ( upon multiplying both sides by -1 ) gives
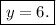
Now we know the value of y. How do we find the value of x and z?
Putting in the value of y into the first and the second equation gives

which gives us
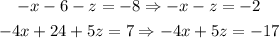
Now our problem has been reduced to two equations and two unknowns.
Solving for x in the first equation above gives
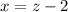
Substituting that into the second equation gives
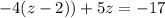
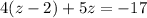
solving fro z gives

with the value of z in hand, we put it into the x = z-2) to get
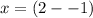

Hence, the solution to the system is
x = 3, y = 6, and z = -1