Question

hello using the kinematic eqautions for the horizontal projectile of a ball being thrown I am given range of flight dx= 1.02time of flight t= 1.20 sheight of launch dy= 1m I need help finding the initial velocity of the realase

Answer 1

intial velocity: 6.02 m /s

Step-by-step explanation:

To find the initial velocity, we make use of the following kinematic equations

`\begin{gathered} y=y_0+(v_0\sin \theta)t-(1)/(2)gt^2 \\ x=(v_0\cos \theta)t \end{gathered}`

Now we know that t = 1.20 s, g = 9.8 m /s, y0 = 1.0 m, and at the ground y =0; therefore, the above equations give

`\begin{gathered} 0=1+(v_0\sin \theta)(1.20)-(1)/(2)(9.8)(1.20)^2 \\ 1.02=(v_0\cos \theta)(1.20) \end{gathered}`

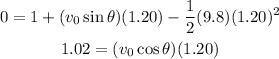
solving these equations for v0 sin θ and v0 cos θ gives

`((1)/(2)(9.8)(1.20)^2-1)/(\mleft(1.20\mright))=(v_0\sin \theta)`
`\Rightarrow v_0\sin \theta=5.05`

and

`(1.02)/(\mleft(1.20\mright))=(v_0\cos \theta)`
`v_0\cos \theta=0.85`

Now dividing the two equations gives

`(v_0\sin \theta)/(v_0\cos \theta)=(5.05)/(0.85)`
`\tan \theta=5.94`

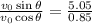
taking the inverse tan gives

`\theta=80.45^o`

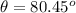
Now that we know theta, it is easy to find v0.

`v_0\sin (80.45)=5.94`
`v_0=(5.94)/(\sin (80.45))`
`\boxed{v_0=6.02}`

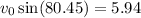
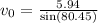
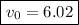
which is our answer!