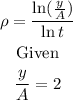Question

See attached pic for problem. Only need help with question C

Answer 1

Doubling time is the amount of time it takes for a given quantity to double in size or value at a constant growth rate. This means that the ratio of the final and initial values of the exponential function will be equal to 2:

`\begin{gathered} \text{For} \\ y=a(b)^x^{} \\ We\text{ have} \\ (y)/(a)=2 \end{gathered}`

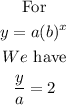
The function is given to be:

`y=At^(\rho)`

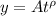
For the doubling time, we have that:

`(y)/(A)=2`

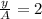
If we divide both sides of the equation by A, we have:

`(y)/(A)=t^(\rho)`

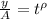
Substituting for the ratio, we have:

`2=t^(\rho)`

Finding the natural logarithm of both sides, we have:

`\ln 2=\ln t^(\rho)`

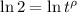
Applying the law of exponents given to be:

`\ln a^b=b\ln a`

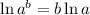
we have that:

`\ln 2=\rho\ln t`

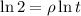
Divide both sides by ln(t), we have:

`\rho=(\ln2)/(\ln t)`

Since we have:

`(y)/(A)=2`

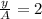
We can have the time to be:

`\begin{gathered} \rho=(\ln ((y)/(A)))/(\ln t) \\ \text{Given} \\ (y)/(A)=2 \end{gathered}`