Question

The endpoints of a diameter are shown on the circle below.Find the center and the length of the radius of the circle. Show all work.

Answer 1

The center of the circle is the midpoint between (3,6) and (5,4). The coordinates of the midpoint are given by:

`\begin{gathered} x=(x_1+x_2)/(2) \\ y=(y_1+y_2)/(2) \end{gathered}`

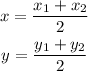
In this case:

(x1,y1) = (3,6)

(x2,y2) = (5,4)

Replace the previous values into the formulas for x and y, and simplify:

`\begin{gathered} x=(3+5)/(2)=(8)/(2)=4 \\ y=(6+4)/(2)=(10)/(2)=5 \end{gathered}`

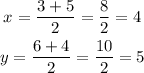
Hence, the center of the given circle is (x,y) = (4,5)

Now, to find the radius of the circle, calcualte the distance between the given points (which is the diameter) and then divide the result by 2.

Use the following formula for the distance between two points:

`\begin{gathered} d=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \\ d=\sqrt[]{(4-6)^2+(5-3)^2} \\ d=\sqrt[]{(-2)^2+(2)^2} \\ d=\sqrt[]{4+4}=\sqrt[]{8}=2\sqrt[]{2} \end{gathered}`

Then, the radius of the circle is:

`r=\frac{2\sqrt[]{2}}{2}=\sqrt[]{2}`