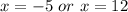Question

Ashley's monthly savings may be modeled by the function f(x) = -2x2 + 14x + 120, where x represents the number of months that have passed

1) Factor the polynomial and 2) identify the zeroes of the function.

Answer 1

The polynomial is given to be:

`f(x)=-2x^2+14x+120`

FACTORING THE POLYNOMIAL

Step 1: Multiply the first and last term of the polynomial and get two numbers that will multiply to give the result and will add up to the middle term

`\begin{gathered} -2x^2*120=-240x^2 \\ Numbers=-10x,+24x \end{gathered}`

Step 2: Replace the middle term with the two numbers gotten in Step 1 above

`f(x)=-2x^2-10x+24x+120`

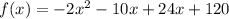
Step 3: Factor out the common term in each pair of numbers as shown below

`\begin{gathered} f(x)=(-2x^2-10x)+(24x+120) \\ f(x)=-2x(x+5)+24(x+5) \end{gathered}`

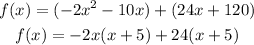
Step 4: Factor out the common term (x + 5)

`f(x)=(x+5)(-2x+24)`

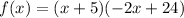
Step 5: Factor out -2x from the term (-2x + 24)

`f(x)=-2(x+5)(x-12)`

The factored polynomial is:

`f(x)=-2(x+5)(x-12)`

ZEROES OF THE FUNCTION

The zeroes of the function are gotten at f(x) = 0

`f(x)=0`

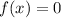
Therefore, we have that:

`-2(x+5)(x-12)=0`

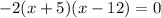
Recall the Zero Factor Principle:

`\begin{gathered} \text{If} \\ ab=0 \\ \text{then} \\ a=0,b=0 \end{gathered}`

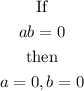
Therefore, we have that:

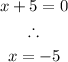
`\begin{gathered} x+5=0 \\ \therefore \\ x=-5 \end{gathered}`

or

`\begin{gathered} x-12=0 \\ \therefore \\ x=12 \end{gathered}`

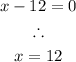
Therefore, the zeroes of the function are:

`x=-5\text{ }or\text{ }x=12`