Question

A 221-gram ball is thrown at a speed of 36.7 m/s from the top of a 39.8-m high cliff. Determine the impact speed of the ball when it strikes the ground. Assume negligible air resistance.

Answer 1

Given:

The mass of the ball is

`\begin{gathered} m=221\text{ g} \\ =0.221\text{ kg} \end{gathered}`

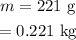
The initial height of the ball is

`h=39.8\text{ m}`

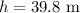
The initial speed of the ball is

`v_i=36.7\text{ m/s}`

To find:

the impact speed of the ball when it strikes the ground

Step-by-step explanation:

The initial potential energy of the ball is

`\begin{gathered} (PE)_i=mgh \\ =0.221*9.8*39.8 \\ =86.2\text{ J} \end{gathered}`

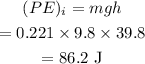
The initial kinetic energy is

`\begin{gathered} (KE)_i=(1)/(2)mv_i^2 \\ =(1)/(2)*0.221*(36.7)^2 \\ =148.8\text{ J} \end{gathered}`

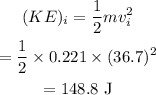
The final energy of the ball is fully kinetic energy. Let the final impact speed of the ball is

`v_f`

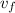
We can write, using the energy conservation principle that

`\begin{gathered} (PE)_i+(KE)_i=(1)/(2)mv_f^2 \\ 86.2+148.8=(1)/(2)*0.221* v_f^2 \\ v_f^2=2*(86.2+148.8)/(0.221) \\ v_f=46.1\text{ m/s} \end{gathered}`

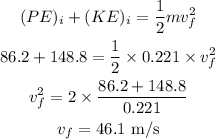
Hence, the final impact speed of the ball is 46.1 m/s.