Question

BCD and LABC are supplementary, What additional condition(s) would make quadrilateralABCD a parallelogram?Select all that apply3cBAC_DCADCS and ZADC are supplementary

Answer 1

A parallelogram:

Opposite angles are equal.

Opposite sides are equal and parallel.

Diagonals bisect each other.

Sum of any two adjacent angles is 180°

A rectangle:

All the angles of a rectangle are 90°

Opposite sides of a rectangle are equal and Parallel.

Diagonals of a rectangle bisect each other.

A rhombus:

Opposite angles are equal.

All sides are equal and, opposite sides are parallel to each other.

Diagonals bisect each other perpendicularly.

Sum of any two adjacent angles is 180°

A square:

The diagonals of a square bisect each other and meet at 90°.

The diagonals of a square bisect its angles.

Opposite sides of a square are both parallel and equal in length.

All four angles of a square are equal

All four sides of a square are equal.

According to the figure:

`\begin{gathered} BC\parallel AD,BC=AD \\ AB\parallel CD,AB=CD \\ \angle A=90 \\ \angle B=90 \\ \angle C=90 \\ \angle D=90 \end{gathered}`

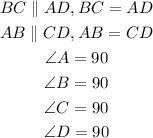
Therefore, we can conclude that the figure is a rectangle and a parallelogram