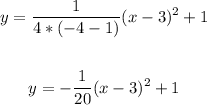vertex (3, 1)
directrix y = 6
The equation of a parabola is
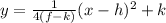
where,
(h,k) is the vertex and (h,f) is the focus
Thus,
h = 3
k = 1
The distance from the focus to the vertex is equal to the distance from the vertex to the directrix, then f - k = k - 6
replace k=1 and solve for f,
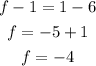
Thus,
h = 3
k = 1
f = -4
therefore, the equation of the parabola is,