Question

F(x) = ^3 square root 3xg(x) = 3x + 2find (f/g) (x). include any restrictions of the domain.

Answer 1

`((f)/(g))(x)\text{ = }\frac{\sqrt[3]{3x}}{3x+2},\text{ x}\\e\text{ -}(2)/(3)`

Step-by-step explanation:

Here, we want to evaluate the function division

Mathematically, we have this as follows:

`((f)/(g))(x)\text{ = }(f(x))/(g(x))\text{ = }\frac{\sqrt[3]{3x}}{3x+2}`

Finally, we need to get the domain restriction

To get the domain restriction, we need to find the value of x under which the denominator becomes zero

Mathematically, we have this as:

`\begin{gathered} 3x\text{ + 2= 0} \\ 3x\text{ = -2} \\ x\text{ = -}(2)/(3) \end{gathered}`

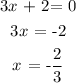
Thus, we have the correct representation as:

`((f)/(g))(x)\text{ = }\frac{\sqrt[3]{3x}}{3x+2},\text{ x}\\e\text{ -}(2)/(3)`