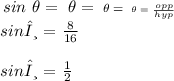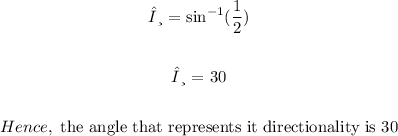Question

When traveling through air, a spherical drop of blood with diameter d maintains its spherical shape until hitting a flat surface. The direction of travel of the drop of blood dictates the directionality of the blood splatter on the surface. For this reason, the diameter of the blood drop is equal to the width of the blood splatter on the surface. The angle at which a spherical drop of blood is deposited on a surface, called angle of impact, is related to the width w and the length l of the splatter by sinθ=wl.If a drop of blood found at a crime scene has a width of 8 millimeters and length of 16 millimeters, find the angle θ that represents the directionality.

Answer 1

Answer:

the angle θ that represents the directionality is 30°

Step-by-step explanation:

Given:

the angle of impact is related to the width w and the length l of the splatter by sinθ = w/l

width = 8 millimeters, length = 16 millimeters

To find:

the angle θ that represents the directionality

We will use the diagram to get the measure of the angle:

`\begin{gathered} sin\text{ \theta = }(opp)/(hyp) \\ \\ sinθ\text{ = }(8)/(16) \\ \\ sinθ\text{ = }(1)/(2) \end{gathered}`
`\begin{gathered} θ\text{ = sin}^(-1)((1)/(2)) \\ \\ θ\text{ = 30\degree} \\ \\ Hence,\text{ the angle that represents it directionality is 30\degree} \end{gathered}`