The Conjugate Zeros Theorem
Given a polynomial with real coefficients, if we know one complex root in the form z = a + bi, then the theorem guarantees there is another root that is the conjugate of z, that is z* = a - bi.
We have the polynomial:
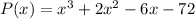
And one of its zeros (roots) is -3 + 3i, then the other complex zero is -3 - 3i.
If we know the value of two of the three zeros of P(x), the other zero can be found by several methods. We'll use the synthetic division.
First, arrange the coefficients of P(x) and prepare the layout of the method:
| 1 2 -6 -72
|
-------------|---------------------------------------
Use the inverse of the first root and apply the sequence of operations as follows:
Take the first 1 down and multiply by -3+3i. It will be placed under the 2. Then add them.
| 1 2 -6 -72
-3 + 3i | -3+3i
--------------|---------------------------------------
| 1 -1 +3i
Take the first 1 down and multiply by -3+3i. It will be placed under the 2. Then add them.
Multiply (-3 + 3i) (-1+3i) = 3-9i-3i-9 = -6 - 12i.
Get it under -6 and add them up:
| 1 2 -6 -72
-3 + 3i | -3+3i -6-12i
--------------|---------------------------------------
| 1 -1 +3i -12 - 12i
Multiply (-3 + 3i) (-12 - 12i) = 36 + 36i - 36i + 36 = 72
Add it with the last coefficient;
| 1 2 -6 -72
-3 + 3i | -3+3i -6-12i 72
--------------|---------------------------------------
| 1 -1 +3i -12 - 12i 0
The last 0 confirms -3 + 3i is a zero of P(x). Now for the other root:
| 1 2 -6 -72
-3 + 3i | -3+3i -6-12i 72
--------------|---------------------------------------
| 1 -1 +3i -12 - 12i 0
-3 - 3i | -3 - 3i 12 +12i
--------------|---------------------------------------
| 1 -4 0
The last polynomial that remains after the two divisions is x - 4
Solving x - 4 = 0
x = 4
The third zero is x = 4