Question

Solve for x. Round to the nearest tenth, if necessary.70B3.6хA

Answer 1

Trigonometric Ratios

The trigonometric ratios stand in every right triangle, i.e. those triangles having one angle of 90°.

The triangle provided in the figure is right because it has a clearly marked angle of 90°. The side opposite to this angle is called the hypotenuse, and the other two sides are called the legs.

We are given the hypotenuse of AC=3.6 units, and the angle C = 70°.

To find the length of the side x, we should use a trigonometric ratio that relates the opposite side of 70° and the hypotenuse.

This ratio is called the sine, defined as follows:

`\displaystyle\sin 70^o=\frac{\text{opposite leg}}{\text{hypotenuse}}`

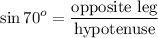
Substituting:

`\displaystyle\sin 70^o=\frac{\text{x}}{\text{3}.6}`

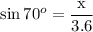
Solving for x:

x = 3.6 sin 70° = 3.6 * 0.9397 = 3.4

x = 3.4 units