Question

The following graphs have no scales assigned to them. Which of them couldbe density curves for a continuous random variable if they were provided withthe right scale?Check all that apply.A. Graph AB. Graph BC. Graph CD. Graph DE Graph E

Answer 1

Given that:

- The graphs have no scales assigned to them.

- You have to identify the ones that could be density curves for a continuous random variable assuming that they have the right scale.

Then, in order to solve this exercise, you need to remember the following:

1. A Probability Density Function is useful to define the probability of a random variable within a distinct range of values.

2. It is also known as PDF.

3. The Probability Density Function is always positive in all its Domain.

4. The total enclosed area under the curve of the function is:

`A=1`

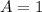
Knowing all these concepts, you can identify that:

- In graph B the area under the curve is 0. Therefore, this cannot be the graph asked in the exercise.

- In Graph C, the function is not positive in its Domain. Therefore, this does not satisfy the properties mentioned before.

Hence, the answers are:

- Option A.

- Option D.

- Option E.