To get the solution to the question, we will attempt to solve the absolute value equation:

Step 1: Subtract 25 from both sides of the equation
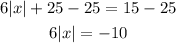
Step 2: Divide both sides of the equation by 6
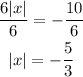
Step 3: Recall that an absolute value is nonnegative, meaning it is either zero or positive. The output of the absolute value operator is never negative. Therefore, there is no solution
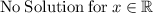
ANSWER: The THIRD OPTION is correct.