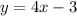A line equation can be written in slope-intercept form, which is

where m represents the slope and b represents the y-intercept.
Parallel lines have the same slope. If we rewrite the given line equation in slope-intercept form and identify the slope, it will be the same slope of our line.
Rewritting the given line equation, we have
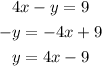
The slope of the given line is equal to 4. Our line equation is
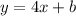
To identify the y-intercept, we can evaluate the given point that belongs to this line.
Evaluating the point, we have
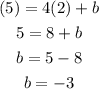
The equation of our line is