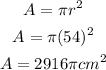Question

Flashlight problem: you shine a flashlight, making a circular spot of light on the wall with radius 5cm. As you back away from the wall, the radius increases at the rate of 7 cm/s. Use the radius at times 4s and 7s to find the area of the spot of light at these times.

Answer 1

We can model the radius function, R(t), with respect to time.

The initial radiusis 5 cm and it increases 7 cm /second, so we can write:

`R(t)=5+7t`

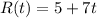
• At ,t = 4 ,second, the radius is:

`\begin{gathered} R(t)=5+7t \\ R(4)=5+7(4) \\ R(4)=5+28 \\ R(4)=33 \end{gathered}`

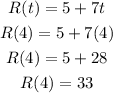
We can find the area of the spotlight by substituting r = 33 into the circle area formula. This is shown below:

`\begin{gathered} A=\pi r^2 \\ A=\pi(33)^2 \\ A=1089\pi cm^2 \end{gathered}`

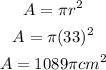
• At ,t = 7 ,second, the radius is:

`\begin{gathered} R(t)=5+7t \\ R(7)=5+7(7) \\ R(7)=5+49 \\ R(7)=54 \end{gathered}`

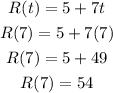
We can find the area of the spotlight by substituting r = 54 into the circle area formula. This is shown below:

`\begin{gathered} A=\pi r^2 \\ A=\pi(54)^2 \\ A=2916\pi cm^2 \end{gathered}`