Question

the table below shows an end of the year inventory report for a warehouse that supplies electronics stores. The warehouse stocks two models of cordless phones. Model A is valued at $75 and Model B at $110. How many if each model did the warehouse have at the time of the inventory? (set up and solve a system of equations to answer this question) item cordless phone number 195merchandise value $17,215

Answer 1

Let x denote the number of model A phones.

Let y denote the number of model B phones.

We can set up two equations with the given information.

The total number of phones in the inventory is 195.

`x+y=195\quad eq.1`

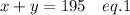
Model A is valued at $75 and Model B at $110 and the total worth of these phones is $17,215.

`75x+110y=17215\quad eq.2`

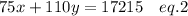
Now we can use the substitution method to find the values of x and y.

From eq. 1, you can separate out any one of the variables and substitute it into eq. 2

`y=195-x\quad eq.1`

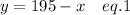
Substitute it into the eq. 2

`\begin{gathered} 75x+110y=17215 \\ 75x+110(195-x)=17215 \\ 75x+21450-110x=17215 \\ 75x-110x=17215-21450 \\ -35x=-4235 \\ 35x=4235 \\ x=(4235)/(35) \\ x=121 \end{gathered}`

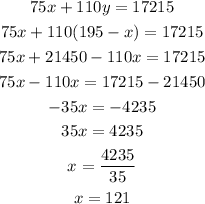
Finally, substitute the value of x into eq. 1 to find the value of y.

`\begin{gathered} y=195-x \\ y=195-121 \\ y=74 \end{gathered}`

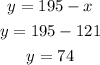
Therefore,

x = 121 the number of model A phones

y = 74 the number of model B phones