you have to increase 0.01 meters the length
Step-by-step explanation
The period of a pendulum is given by:
![T=2\text{ }\pi\sqrt[]{(L)/(g)}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/a1yd6v1hsa6zbneoe19i.png)
where T is the period, L is the length , a g is the the acceleration of the gravity (9.8 m per square second)
s
Step 1
find the length, for period= 2 s
Let
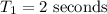
with this value, we can find the length
replace, and isolate L
![\begin{gathered} T=2\text{ }\pi\sqrt[]{(L)/(g)} \\ 2=2\text{ }\pi\sqrt[]{(L)/(g)} \\ \text{divide both sides by 2}\pi \\ (2)/(2\pi)=\frac{2\text{ }\pi}{2\pi}\sqrt[]{(L)/(g)} \\ (1)/(\pi)=\sqrt[]{(L)/(g)} \\ ((1)/(\pi))^2=(\sqrt[]{(L)/(g)})^2 \\ (1)/(\pi^2)=(L)/(g) \\ \text{Multiply both sides by g} \\ (1)/(\pi^2)\cdot g\cdot g=(L)/(g) \\ (g)/(\pi^2)=L \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/aarl5udjobd1era1yg1i.png)
so, when the period is 2.00 s the length of the pendulum is
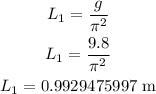
Step 2
now, for Period = 1.99 s
Let

replace and solve for L
![\begin{gathered} T=2\text{ }\pi\sqrt[]{(L)/(g)} \\ 1.99=2\text{ }\pi\sqrt[]{(L)/(g)} \\ \text{divide both sides by 2}\pi \\ (1.99)/(2\pi)=\frac{2\text{ }\pi}{2\pi}\sqrt[]{(L)/(g)} \\ (1.99)/(2\pi)=\sqrt[]{(L)/(g)} \\ ((1.99)/(2\pi))^2=(\sqrt[]{(L)/(g)})^2 \\ \\ 0.1003105048=(L)/(g) \\ \text{Multiply both sides by g} \\ 0.1003105048\cdot g=(L)/(g)\cdot g \\ 0.1003105048\cdot g=L \\ L=0.1003105048\cdot9.8 \\ L_2=0.983049474\text{ m} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/a6b3g6d5exc0r10r88ja.png)
so, when the period is 1.99 s , the length is 0.9830429474 m
Step 3
finally, to know how much you must increase the length, subtract L2 from L1
so
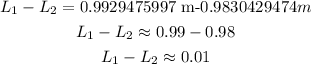
therefore, the make the pendulum osscilates with period of 2 seconds, you have to increase 0.01 meters the length
I hope this helps you