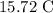Given:
the mass of the ice is
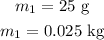
the temperature of the ice is

The specific heat of the ice is
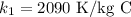
latent heat of the ice is

The mass of the water is
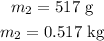
The temperature of the water is
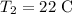
Specific heat of the water is
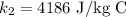
The mass of the copper is
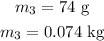
The temperature of the copper is
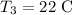
and specific heat of the copper is

Required: the final temperature
Step-by-step explanation:
to solve this problem we will use the concept of calorimetry
that is given as
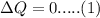
froheat required to melt the ice form -73 to 0 is given by
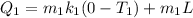
plugging all the values in the above relation we get
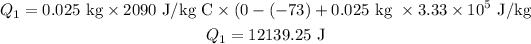
now calculate for whole system
heat required to increase the temperature of melted ice is
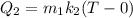
heat required water to increase its temperature
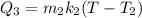
heat required to increase the temperature of the copper is
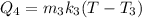
now from the equation (1)
![\begin{gathered} Q_1+Q_2+Q_3+Q_3=0 \\ 12139.25\text{ J +0.025}*4186(T-0)+0.517\text{ kg}*4186\text{ J/kg}(T-22)+0.074\text{ kg}*387\text{ J/kg C }((T-22)=0 \\ T=(36102)/(2297.29) \\ T=15.72\text{ C} \end{gathered}]()
Thus, the final temperature of the system is