Question

pls help! Find the measure of the arc or angle indicatedFind the measure of mCDa) 35°b) 133°c) 120°d) 127°

Answer 1

In the figure, we can see that the angle is inside the circle but its vertex, B, is not the center of the circle. The sides of the angle intercept with two arcs, arc EJ and arc CD. The measure of the angle has the following relationship with the intercepted arcs:

The measure of the angle is equal to half the sum of the intercepted arcs.

For the given circle, the measure of the angle is equal to:

`109x+1=(1)/(2)(127x+93)`

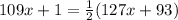
From this expression, we can determine the value of x.

-First, distribute the multiplication on the parentheses term:

`\begin{gathered} 109x+1=(1)/(2)\cdot127x+(1)/(2)\cdot93 \\ 109x+1=63.5x+46.5 \end{gathered}`

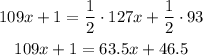
-Second, pass the x-term to the left side of the equation by applying the opposite operation to both sides of the equal sign. Repeat to pass the 1 to the right side of the equation.

`\begin{gathered} 109x-63.5x+1=63.5x-63.5x+46.5 \\ 45.5x+1=46.5 \end{gathered}`
`\begin{gathered} 45.5+1-1=46.5-1 \\ 45.5x=45.5 \end{gathered}`

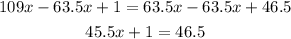
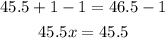
-Third, divide both sides of the expression by 45.5 to determine the value of x:

`\begin{gathered} (45.5)/(45.5)x=(45.5)/(45.5) \\ x=1 \end{gathered}`

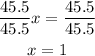
Now that we know the value of x, we can determine the measure of arc CD

`\begin{gathered} mCD=127x \\ mCD=127\cdot1 \\ mCD=127º \end{gathered}`

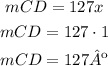
So mCD=127º