The tables represent the linear relationship between the rental cost (y) of a surfboard with respect to the time (x) for two beachfront stores "Hang Ten" and "Waverider"
To determine the equations that represent the linear relationship between the rental cost and the rental time for each shop, the first step is to determine the slope of the line using the following formula:
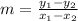
Where
m is the slope
(x₁,y₁) are the coordinates of one point of the line
(x₂,y₂) are the coordinates of a second point of the line
For this example, the variable time (x) is the independent variable, i.e. it represents the variable in the x-axis. And the variable rental cost (y) is the dependent variable represented by the values of the y-axis.
The second step, once the slope is calculated, is to use the point-slope form to calculate the equation of each line.
For "Hang Ten"
First step: Calculate the slope
To calculate the slope you have to choose any two ordered pair of the table, for example, (3,68) and (2,48) and replace them in the formula above:
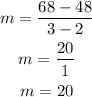
The slope of this line is m=20$/h
Second step: Using the point-slope form you can determine the equation of the line.
The point-slope form is:

Where
m is the slope
(x₁,y₁) are the coordinates of one point of the line
Using the point (1,28) and the slope m=20, the equation of the line is:
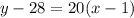
You can express it in slope-intercept form by writing the equation in terms of y.
For this, first, you have to distribute the multiplication on the parentheses term:
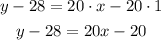
Then pass -28 to the right side of the equation by applying the opposite operation +28 to both sides of it:
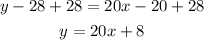
The equation that represents the relationship between the rental cost of a surfboard and the time it was rented at the shop "Hang Ten" is y=20x+8
For "Waverider"
First step: calculate the slope
Same as what we did for the first store, you have to choose two ordered pairs from the table of prices of this store and replace them in the formula to calculate the slope.
I will use the ordered pairs (4,97) and (3,80)
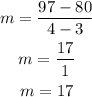
The slope for this relationship is 17$/h
Second step: using the point-slope form you can determine the equation of the line:
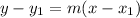
Where
m is the slope
(x₁,y₁) are the coordinates of one point of the line
Using the point (2,63) and slope m=17 the equation for the line is:
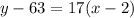
As before, let's express it in slope-intercept form.
First, distribute the multiplication on the parentheses term
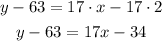
Second, pass -63 to the right side of the equation by applying the opposite operation, +63, to both sides of it:
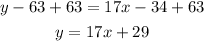
The equation that represents the linear relationship between the rental cost of a surfboard and the time for the shop Waverider is: y=17x+29
So we have determined the system of linear equations
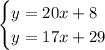
To determine the time when both services will have the same cost, you have to equal both equations and solve for x:

First, pass the x-term to the left side of the equation by applying the opposite operation to both sides of it. Repeat it to pass 8 to the left side of the equation.

Second, since the x-term is multiplied by "3", you have to divide it by 3 to cancel the multiplication, and, to keep the equality valid, any operation done to one side of the equal sign must be done to the other side, so you have to divide 21 by 3 too:
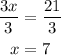
This means that at 7 hours of the rental, the cost for both services will be the same.
Finally, to determine the said cost, you have to replace either equation with x=7 and calculate for y:
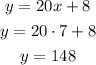
The cost for renting a surfboard for 7 hours will be $148 for both shops.