Question

Compare compare post to be below having to do with Ben's

Answer 1

Given the voting system {17:14, 5, 2}

The coalitions, their weight, critical player and if they win or loose will be presented below

From the table above, the only coalition cases we have win are {14+5} and {14+5+2}, Player with weight 14 is critical two times, while playerwith weights 5 is critical twice and player with weight 2 is never critical, thus the following extraction can be made

`\begin{gathered} T\Rightarrow\text{The total number of times players are critical = }4 \\ B_(14)\Rightarrow\text{ the number times player 14 is critical= 2} \\ B_5\Rightarrow\text{ the number times player 5 is critical= }2 \\ B_2\Rightarrow\text{the number times player 2 is critical= }0 \end{gathered}`

Given the formula for the Banzhaf power index for a player to be;

`P_i=(Bi)/(T),\Rightarrow\begin{cases}P_i\Rightarrow\text{ player index} \\ B_i\Rightarrow\text{ the number times player is critical} \\ T\Rightarrow\text{ the total number times players are is critical}\end{cases}`

Thus to calculate the Banzhaf for each player we have

`\begin{gathered} P_(14)=\beta_1=(B_(14))/(T)=(2)/(4)=(1)/(2) \\ P_5=\beta_2=(B_5)/(T)=(2)/(4)=(1)/(2) \\ P_2=\beta_3=(B_2)/(T)=(0)/(4)=0 \end{gathered}`

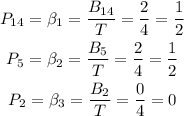
Hence, the Banzhaf power distributions are

`\beta_1=(1)/(2),\beta_2=(1)/(2),\beta_3=0`

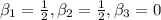
b) Given the voting system {19: 16, 9, 1}

The winning coalitions and their respective critical players is given below

`\begin{gathered} \mleft\lbrace16,9\mright\rbrace\Rightarrow critical\text{ player (16,9)} \\ \mleft\lbrace16,9,1\mright\rbrace\Rightarrow\text{ critical players (16,9)} \end{gathered}`

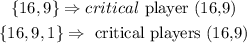
From the table above, the only coalition cases we have win are {16,9} and {16,9,1}, Player with weight 16 is critical two times, while playerwith weights 9 is critical twice and player with weight 1 is never critical, thus the following extraction can be made

`\begin{gathered} T=2+2+0=4 \\ B_(16)=2 \\ B_9=2 \\ B_1=0 \end{gathered}`

The Banzhaf distribution fo the voting sysytem is

`\begin{gathered} \beta_1=(B_(16))/(T)=(2)/(4)=(1)/(2) \\ \beta_2=(B_9)/(T)=(2)/(4)=(1)/(2) \\ \beta_3=(B_1)/(T)=(0)/(4)=0 \end{gathered}`

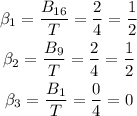
Hence, the Banzhaf distribution power is

`\beta_1=(1)/(2),\beta_2=(1)/(2),\beta_3=0`

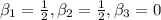
Conclusion, the Banzhaf power distributions are the same in both (a) and (b),

Option D is right answer