ANSWER
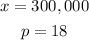
Step-by-step explanation
The point of equilibrium for the demand and supply function is the point where the demand price is equal to the supply price.
This implies that the functions are equal:

Now, we can find the value of x, the number of units for equilibrium by simplifying the equation:
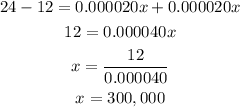
That is the number of units for equilibrium.
To find the price per unit at equilibrium, solve for p using either function.
Let us make use of the demand function:
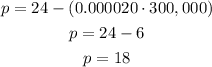
That is the price per unit at equilibrium.